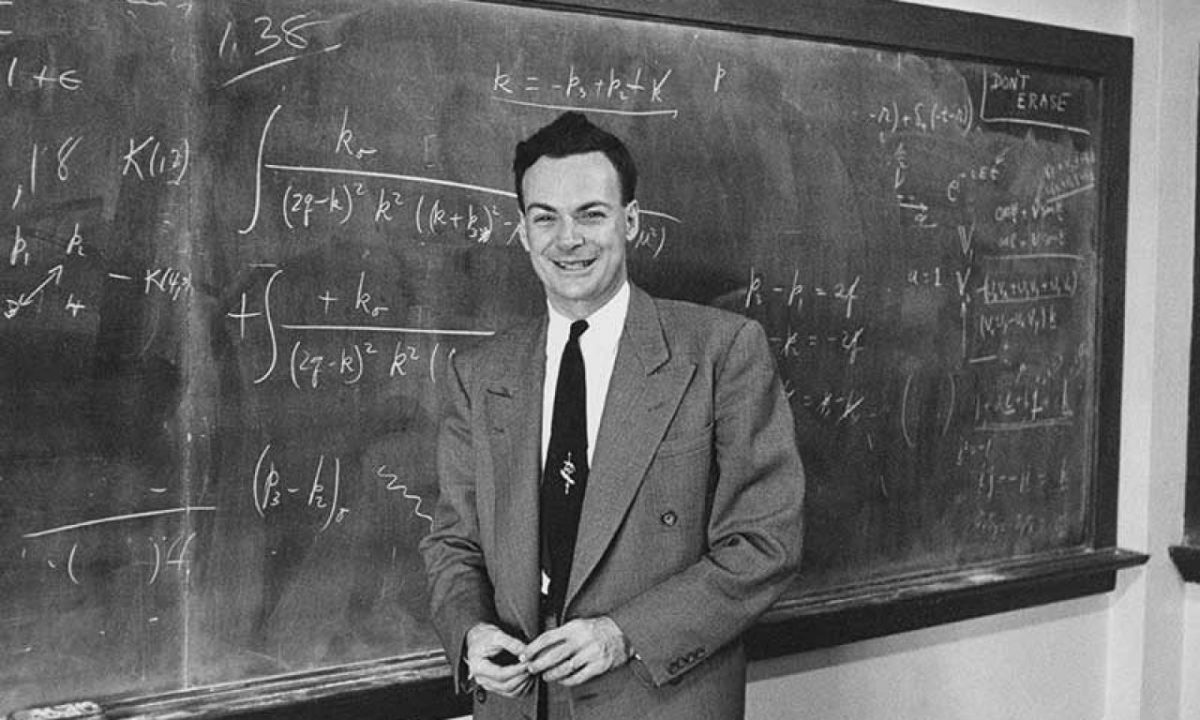Las leyes de la física cuántica se aplican al mundo de las partículas elementales del mismo modo que las leyes de la mecánica clásica se aplican al mundo macroscópico. Hace medio siglo (1954), Yang y Mills introdujeron un nuevo marco extraordinario para describir las partículas elementales utilizando estructuras que también se dan en la geometría. La teoría cuántica de Yang-Mills es ahora el fundamento de la mayor parte de la teoría de las partículas elementales, y sus predicciones se han puesto a prueba en muchos laboratorios experimentales, pero su fundamento matemático sigue sin estar claro. El éxito de la teoría de Yang-Mills para describir las interacciones fuertes de las partículas elementales depende de una sutil propiedad mecánica cuántica llamada brecha de masa (mass gap): las partículas cuánticas tienen masas positivas, aunque las ondas clásicas viajen a la velocidad de la luz. Esta propiedad ha sido descubierta por los físicos a partir de experimentos y confirmada por simulaciones informáticas, pero aún no se ha entendido desde un punto de vista teórico. Los avances en el establecimiento de la existencia de la teoría de Yang-Mills y de una brecha de masa requerirán la introducción de nuevas ideas fundamentales tanto en física como en matemáticas. [2]
Continuar leyendo «Los problemas del milenio – P1: Campo de Yang-Mills y el salto de masa»Los problemas del milenio: Germen
En esta serie de publicaciones estaré presentando los siete Problemas del Milenio anunciado por el Instituto Clay de Matemáticas en el 2000, la cual se hizo inmediatamente conocida y tuvo una gran repercusión en todo el mundo, por la importante contribución en las matemáticas y en otras áreas, como la jugosa compensación de $ 1.000.000 (un millón de dólares americanos).
La idea es tratar de explicar de la forma más concreta posible, ya que en algunos casos no puede reducirse a una simpleza para la cual comprenda cualquier que no esté muy relacionado con las matemáticas. Incluso el enunciado podría ser complicado de entender.
Continuar leyendo «Los problemas del milenio: Germen»Artificio de Feynman para integrales
Continuar leyendo «Artificio de Feynman para integrales»“Había aprendido a hacer integrales mediante varios métodos que se muestran en un libro que me había dado el profesor de física de mi escuela secundaria, el Sr. Bader. [Mostró] cómo diferenciar parámetros bajo el signo integral: es una operación determinada. Resulta que eso no se enseña mucho en las universidades; no lo enfatizan. Pero descubrí cómo usar ese método, y usé esa maldita herramienta una y otra vez. [Si] los chicos del MIT o Princeton tenían problemas para hacer una determinada integral, [entonces] yo venía y trataba de diferenciar bajo el signo de integral, y a menudo funcionaba. Así que obtuve una gran reputación por hacer integrales, solo porque mi caja de herramientas era diferente a la de los demás, y ellos habían probado todas sus herramientas antes de plantearme el problema». (¡Seguro que está bromeando, señor Feynman!)
https://medium.com/cantors-paradise/richard-feynmans-integral-trick-e7afae85e25c
Función gama, o una generalización de los factoriales
Daniel Bernoulli define una extensión de los factoriales que se define como para
, es más, para números complejos con parte real positiva, así se define la función gama
Veamos porqué esta función puede ser una extensión para los factoriales. Para ello debe cumplirse que para
. Sea
, entonces
Una indeterminación puede valer cualquier cosa
En análisis o cálculo habrás visto el caso de las indeterminaciones, preguntándote por qué algo tan simple como puede resultar distinto de cero o cómo
no es 1. Lo cierto es que
no es un número real (¿puede ser otra clase de número? sí) y esto trae consecuencias negativas en los cálculos, lo que sí es en el conjunto
tiene por fundamento justo la indeterminación de su valor. Es decir, tiene por definición la expresión que no tiene fin, esto es, no existe un número superior a éste.
En análisis, cuando consideramos números que tienden a infinito, muchas veces podríamos abreviar cuando
simplemente por
. ¿Lo ves? Ya no parece un número.
Factorial infinito
Buscaremos ahora un valor para la expresión . Recuérdese que
. Ahora,
Aplicando logaritmo en cada miembro nos queda
Consideremos ahora la función zeta de Riemann,
derivando nos queda . En particular, para
, se tiene
donde , por tanto de (1) y (2), tenemos la relación
Aplicando la función exponencial
Pero claro, también puede valer .
Sumatorio de Ramanujan
Otro resultado similar es el de la suma de Ramanujan, el cual fue descubierto en uno de sus cuadernos. En general, la suma de Ramanujan se puede expresar como

Ramanujan, probando de la forma más simple considera la suma infinita
Restando en este orden
Considerando ahora la serie de Taylor , cuando
. Así
.
Luego . Por tanto
Principio de inclusión-exclusión
Consideremos dos conjuntos cualesquiera, si queremos saber cuántos elementos tiene la unión simplemente contamos los elementos de
y los elementos de
y lo sumamos, y en el caso en el que exista algún elemento en la intersección simplemente lo excluimos, así denotando
a la cardinalidad de un conjunto
, tenemos que se cumple
sin importar si en la intersección hubiese algún elemento, ya que la cardinalidad de vacío es cero.

Esperando en la fotocopiadora descubre la teoría de ondículas-Premio Princesa de Asturias 2020
Dos franceses, una belga y un australiano ganan el Premio Princesa de Asturias en Investigación Científica y Técnica por sus teorías, que ayudan a entender un cuadro de Van Gogh o a construir imágenes para un diagnóstico médico. Estos cuatros galardonados tienen algo en común, todos son matemáticos.
La compresión de archivos gráficos sin apenas perder resolución (como un cuadro de Van Gogh), la reconstrucción de imágenes para el diagnóstico médico o las técnicas para visualizar y escuchar el universo están empapadas de matemáticas, elemento transversal de todas las ramas de la ciencia y el ADN de la era digital. Las teorías y técnicas para el procesamiento matemático de datos han sido hoy protagonistas del premio Princesa de Asturias de Investigación Científica y Técnica 2020 que ha recaído en Yves Meyer, Ingrid Daubechies, Terence Tao y Emmanuel Candès, cuatro pioneros en convertir las matemáticas en herramienta universal. Sus contribuciones han ampliado extraordinariamente la capacidad de observación de nuestros sentidos y son la base y soporte de la moderna era digital, según el jurado.